The main elements on the KM pane for model fitting are:
Fit current region |
Starts the process which fits the model curve to the measurements of the selected regional TAC. For compartment models the fit is an iterative optimization, while for other models only a single calculation may be sufficient. In case randomized fitting with a number n of trials is enabled, the button text is changed to Randomized fit current region[n]. |
Fit all regions |
Performs fitting for all TACs of the study using the current regional model definitions. In case randomized fitting with a number n of trials is enabled, the button text is changed to Randomized fit all regions. |
Fit blood param |
If this box it is checked, all parameters of the Input curves which have the fit box checked are also included into the set of fitted parameters. This feature has two uses:
|
Fitting and Initial Parameter Values
Except for linear and multi-linear regression, minimization of the Chi square expression requires an iterative approach. The procedure starts with a set of initial parameter values, generates the corresponding model curve, calculates the Chi square criterion, and adjusts the model parameters such that Chi square is expected to be reduced. The cycle
is then repeated until a further reduction of Chi square is not any more possible. The final set of parameters upon termination is regarded as the best-fit result. It is not analytically exact and may depend on the initial parameters, on the optimization procedure, and on the termination criterion of the iterations. Fitting is started using the Fit current region button.
It is recommended to provide a set of reasonable parameter values at the start of the optimization procedure. If the initial parameters are too far from the optimal solution, there is a higher danger of getting stuck in a local minimum. When fitting complex models, it may be worthwhile to first start with a simpler model and derive initial values from those results.
Automatic Parameter Initialization and Randomized Fitting
The Extras pane contains some settings related to fitting.
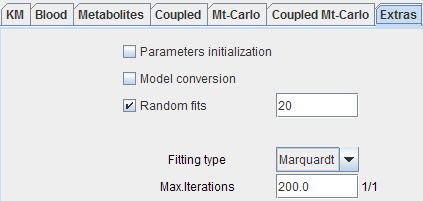
Parameters |
This configuration is only related to the compartment models and determines which initial values are used for the iterative fitting:
|
Model |
This configuration is only related to the compartment models and determines the behavior if the user switches the model between different compartment models:
|
Random |
This configuration is only related to models which require iterative fitting:
Note: The purpose of randomized fitting is to avoid local minima, but there is a chance that the returned solution may contain unphysiologic parameter combinations. |
Fitting |
Selection of the numerical optimization method applied for iterative fitting:
The iterative optimizations terminate, when no substantial improvement can be found any more, or when the Max iterations restriction is hit. Note: Several models (linear and multi-linear regression) are not fitted iteratively because they have closed form solutions. In these cases the Fitting type settings are not relevant. |
Max. |
Maximal number of iterations which are allowed in the Marquardt and Powell fitting. |
Potential Fitting Problems
In the case of a failed fit it is worthwhile to check the console output. For example, the output text reproduced below clearly indicates that the 4th fit parameter caused a problem.
Singular Matrix-2
covar[1][1] = 2.1652603147908747E-6
covar[1][2] = -5.120936302955895E-4
covar[1][3] = 2.862241687078937E-7
covar[1][4] = 0.0
covar[2][1] = -5.120936302955895E-4
covar[2][2] = 0.3918087002588389
covar[2][3] = -2.0406232308544742E-4
covar[2][4] = 0.0
covar[3][1] = 2.862241687078937E-7
covar[3][2] = -2.0406232308544742E-4
covar[3][3] = 1.4044964781403112E-7
covar[3][4] = 0.0
covar[4][1] = 0.0
covar[4][2] = 0.0
covar[4][3] = 0.0
covar[4][4] = 0.0
Such problems might be caused by initial values very close to parameter restrictions.