Monte Carlo Simulations

The purpose of performing Monte Carlo simulations in kinetic modeling is to get information about the standard error of the parameter values found in a fit. There are two different kinds of sources which contribute to the uncertainty of the parameters:

1. All the input data are measured and hence prone to measurement errors.
2. The model may contain more parameters than supported by the data, so that the effect of one parameter may be counter-balanced by another parameter.

The paradigm used for performing Monte Carlo simulations is described by Flannery et al. [11] . The basic idea is to simulate a series of measurements and statistically analyze the results when modeling these synthetic "measurements".

In PKIN Monte Carlo simulations can be performed for compartment models applied to a single tissue (Mt-Carlo) and models coupled across several tissues (Coupled Mt-Carlo) by selecting the respective panes.

Single Tissue

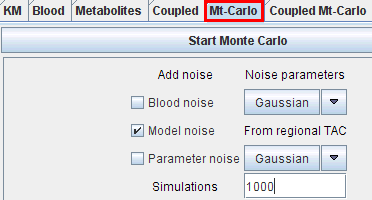
Three types of "noise" can be defined:

1. Blood noise to be added to the blood data for simulating noisy input curves. This option is only supported for blood models of type Measured.
2. Model noise to be added to the tissue model curve for simulating TAC noise. Note that on the KM pane the configured noise can be visualized by checking the Show noise box.
3. Parameter noise to be added to the starting parameters for disturbing the starting conditions from the ideal solution. It is recommended to select the L*y weighting, for instance with L=0.2 to add 20% noise to the ideal parameter value.

Blood and parameter noise can be defined in the Mt-Carlo pane itself using the respective multi-function noise buttons. The noise for the model curve must be defined on the KM pane of the particular region with the Weighting button.

Three distributions are available for noise generation, Gaussian, Poisson and Uniform. They are applied for each individual measurement with a standard deviation calculated as explained above. There are definitions with constant standard deviations for all time points, and others with variable standard deviations.

The standard deviation of the Poisson distribution is determined by the absolute value of y, and is equal to sqrt(y). This way of calculating the standard deviation would be adequate for radioactivity counting, but it is meaningless for the reconstructed values in PET. The following calibration approach is therefore applied: A number can be entered which specifies the relative error of the average measurement, since this is a figure which can be approximately determined. Specifying 0.05, for instance, means a 5% standard error of the mean activity value. The standard deviations of the individual measurements are then calculated accordingly. Note that the Poisson weighting is variable by nature.

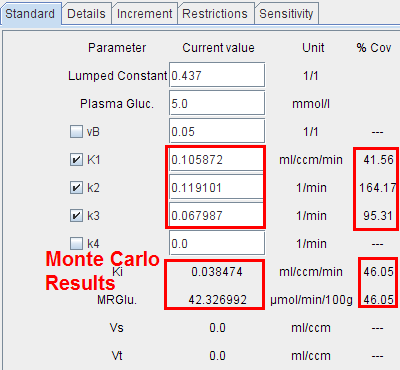
When the Start Monte Carlo button is selected the following processing starts:

1. An initial fit is performed. From then on it is assumed that the result parameters represent the "true" parameters, and the model curve represents the "true" measurement curve.
2. The number of Simulations times a noisy data set is prepared according to the definitions and then fitted. Noise is added to the "true" curve (and optionally the input curve). The "true" parameters, optionally disturbed by some noise, are used as starting values, and the fit to the noisy data performed. The resulting parameter values are recorded.
3. After all runs have completed, the distribution of the result parameters is analyzed resulting in a mean and a standard deviation value for each fitted parameter. These values are shown on the KM page, and the model curve with the mean parameters is shown. Often, it does not follow the measurement as well as with the fitted parameters. The Monte Carlo results should now be saved, because as soon as a parameter is changed or a new fit is initiated, the results get overwritten.
   

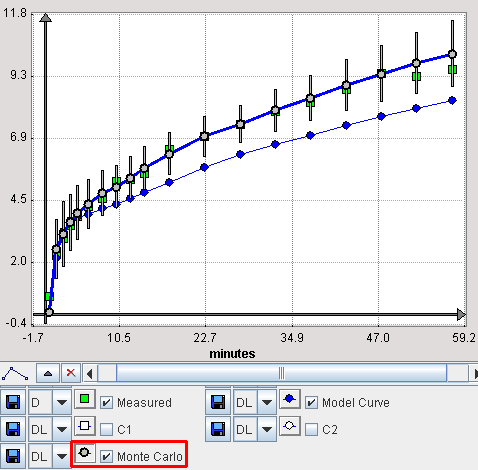
It is possible to visualize a summary of the fit results during the Monte Carlo runs by switching back from the KM to the Mt-Carlo pane. In the curve display, a new curve Monte Carlo appears with vertical bars. The end points of these bars mark the minimal and the maximal value that any of the resulting model curves reached at a particular time point.

Several Tissues Coupled

The same principle as for the single tissue Monte Carlo simulation applies to the Coupled Monte Carlo simulation (Coupled Mt- Carlo tab). In the upper section, the coupled parameters and the regions to couple are defined. In the lower section, blood and parameter noise can be specified. When starting, an initial coupled fit is performed to find the "true" parameters and the "true" model curves. Then, noisy curves are generated and coupled fits performed. At the end, the mean and standard errors are available as the regional parameters.