2-Tissue Compartment Model including Receptor Saturation

This is a standard receptor-ligand model with two tissue compartments defined by

C₁ represents free and non- specifically bound tracer in tissue, and C₂ tracer bound to the receptors. The model accounts for the saturation of receptor sites due to a low specific activity S_act of the injected tracer. In this situation, k₃ is given by k_on(B_max-C₂/S_act), and hence is time-dependent. B_max is the total receptor concentration, k_on the bi-molecular association rate, and k₄ the dissociation rate constant k_off.

System of differential equations [10]:

2-Tissue Compartment by Linear Least Squares Method

As described above the 2-tissue compartment model can be described by the linear arrangement of compartments

and the system of differential equations:

Given the input curve C_plasma(t) and a set of model parameters K₁, .. , k₄, the tissue concentrations C₁(t) and C₂(t) can be calculated by integration of the equation system. However, alternative solutions of the system are possible. With linearized solutions, the equations are integrated twice on both sides, substitutions performed and finally rearranged. This can be done in different ways. The Linear Least Squares method implemented in PKIN uses the derivation of Cai et al. [57], equation (6):

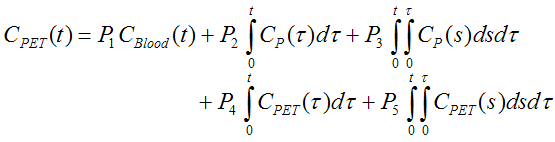
Note that the tissue curve C_PET(t) which is the target function appears on both sides of the equation. It also includes whole-blood activity C_Blood(t) for spillover correction as well as the input curve C_P(t). This multi-linear expression can be solved in a least squares sense in one step without iterations. The present implementation uses a singular value decomposition method. As a result the 5 parameters P₁, .. , P₅ are obtained from which the target parameters can be calculated as follows: [57], equation (9)

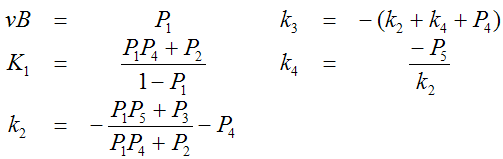
Recommended Use of the Linear Least Squares Method

aThe advantage of the linearized approach is the fast calculation, a well-defined solution, and no danger to get stuck in a local minimum such as the iterative methods. However, it is well known that it is susceptible to bias, and that small TAC perturbations can cause large changes of the parameter estimates. Therefore it is recommended that the Linear Least Squares method is only used for getting a quick solution which is further refined by the iterative methods. In fact, if Parameters Initialization is configured in Extras, the initial starting parameters of the compartment models are obtained by the Linear Least Squares method.

Implementation Notes

The Linear Least Squares method can be used for different model configurations:

• Irreversible model: if k₄ is disabled from fitting, the program automatically sets k₄ = 0. and uses a linearized equation which is modified accordingly.
• 1-tissue compartment model: if k₃ is disabled from fitting, the program automatically sets k₃ = k₄ = 0 and uses a modified equation.
• In all configurations the vB parameter can optionally be disabled from fitting and fixed at a specific user-defined value.