Flumazenil Triple-injection Model

The model developed by Delforge et. al [26] for ¹¹C-Flumazenil consists of two parallel compartment models

They are linked by common model parameters and the system of differential equations

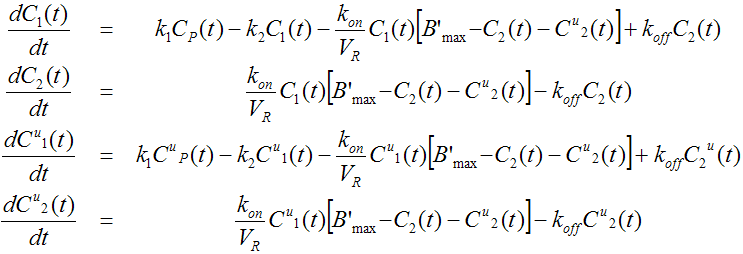
It is important to understand that only the labeled ligand can be measured, both in PET and in blood sampling. This has consequences:

• The input curve of unlabeled ligand must be derived from the input curves of labeled ligand.
• Only the compartments in the upper model can be used for forming the operational equation

The task to derive the input curve is further complicated by the fact of metabolite buildup in plasma which must be corrected for. The input curves must be calculated from the plasma samples C_plasma(t) as follows. Let T₁, T₂ and T₃ be the time of the three injections.

Input curve C_p(t) of hot (labeled) tracer is given by the following expression

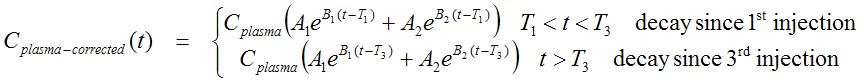
which has been implemented as the input curve model Multiinjection, HOT.

Input curve C^u_p(t) of cold (unlabeled) tracer is given by the expression

which has been implemented as the input curve model Multiinjection, COLD.

Acknowledgement

The model implementation was supported in helpful discussions by Dr. Philippe Millet, University Hospital Geneva, Switzerland [31].

Abstract [26]

"A kinetic method using a multiinjection protocol, positron emission tomography (PET), and [11C]flumazenil as a specific ligand was used to study in vivo the flumazenil-benzodiazepine receptor interactions in the human brain. The model structure is composed of three compartments (plasma, free, and bound ligand) and five parameters (including the benzodiazepine receptor concentration). The arterial plasma concentration, after correction for metabolites, was used as the input function. The experimental protocol, which consisted of three injections of labeled and/or unlabeled ligand, allowed the evaluation of the five model parameters in various brain regions from a single experiment. In particular, the concentration of receptor sites available for binding (B'_max) and the equilibrium dissociation constant (KDVR, VR being the volume of reaction) were estimated in five brain regions, including the pons, in which these parameters are identified for the first time (B'_max = 4.7 +/- 1.7 pmol/ml and KDVR = 4.4 +/- 1.3 pmol/ml). Due to the large range of measured receptor concentrations, a linear correlation between B'_max and KDVR was pointed out (r = 0.88, p < 0.0005) and was interpreted as a linear relationship between B'max and VR, the parameter KD being assumed constant. This result and its concordance with the published data are discussed. Simulation of the usual two-experiment Scatchard analysis, using the pons as a reference region, showed that the bias on the receptor concentration estimates introduced by this method is significant (from 20 to 40%) but can be corrected using an estimate of the receptor concentration in the pons. Furthermore, we propose a new experimental protocol, based on a Scatchard analysis of the PET data obtained with a partial-saturation experiment. This single-injection protocol is entirely noninvasive, and thus the estimation of the benzodiazepine receptor concentration and of the flumazenil affinity is now possible in human patients using a single 1-h experiment without blood sampling."