Previous Topic

Next Topic

Book Contents

Book Index

Simplified Reference Tissue Model 2 (SRTM2)

Model Configuration and Assumptions

The Simplified Reference Tissue Model 2 (SRTM2) was derived by Wu and Carson [1] from the SRTM with the aim of improved parametric mapping. The model structure is the same

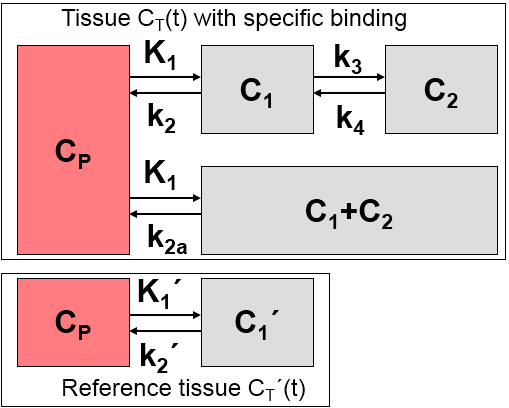
as well as the assumptions:

  1. The distribution volume is the same for the tissue of interest and the reference tissue: K1/k2=K1'/k2'.
  2. The kinetics in the receptor-rich tissue of interest is such, that it is difficult to distinguish between the specific and the free/non-specific compartment; ie. the TAC can be fitted by a 1-tissue compartment model with an uptake rate constant k2a = k2/(1+BPND).

Operational Model Curve

The operational equation of the SRTM was re-written to allow for fixing of k2'. This is relevant for parametric mapping because the model in each pixel TAC uses the same reference TAC and therefore should employ the same k2'. Defining the ratio of tracer delivery R1 as K1/K1' and the binding potential BPND as k3/k4, the following operational equation can be derived for the measured TAC in a receptor-rich region:

Equation SRTM2

The three unknowns R1, k2 and k2a in this equation can be fitted using nonlinear regression techniques. The binding potential can then be calculated as

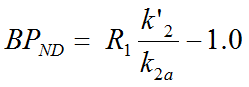
Equation SRTM2 BP

For convolution with the exponentials, the reference tissue TAC CT'(t) is resampled on a regular grid, which can be specified by the Resampling parameter.

Parameter Fitting

The operational equation includes three unknowns: R1, k2, and k2a which can be fitted using nonlinear fitting techniques. Note that k2', the transfer of tracer from the reference tissue back to the plasma, can also be fitted. This can be employed by first estimating k2' with a coupled fit and adequate TACs, and then fixing it for all regional fits as described above. Furthermore, fixing of k2' allows studying the bias introduced by an inadequate k2'.

Note: As with the SRTM method, BPND estimates from SRTM2 tend to be biased if the 1-tissue compartment model assumption does not apply. The magnitude of the bias is even larger, most likely because the fixed k2' can not compensate any more a part of the model inadequacy.

Reference

1. Wu Y, Carson RE: Noise reduction in the simplified reference tissue model for neuroreceptor functional imaging. J Cereb Blood Flow Metab 2002, 22(12):1440-1452. DOI