The Card. Rb82(1 Compartment) model has been developed by Lortie et al. [1] for cardiac PET studies using 82Rb bolus injection. It is based on a 1-tissue compartment model with plasma activity CP(t) and total uptake in myocardium Cmyo(t).
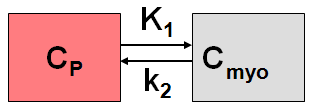
Operational Model Curve
The differential equation is given by
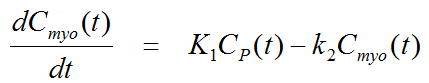
The model uses the activity in the left ventricular cavity Clv(t) is used as the input curve (CP(t)=CLV(t)). Rb is known to have a flow-dependent extraction fraction, so that K1, which is the product of flow F times extraction fraction E, is described by the expression
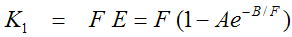
This expression is inserted for K1 into the differential equation, so that F becomes a fit parameter, and K1 is derived from it. The values of the extraction parameters reported by Lortie et al. [1] are
A = 0.77
B = 0.63 [ml/min/g]
They can be entered as input parameters into the model for changing the form of the extraction function. The model curve incorporates a cardiac dual spillover correction, resulting in the operational equation
![]()
where
VLV = spill-over fraction of the blood activity in the left ventricular cavity CLV(t),
VRV = spill-over fraction of the blood activity in the right ventricular cavity CRV(t)
Implementation
When using the model from the PCARD module, the data are transferred appropriately. When using it in PKIN the blood data have to be loaded as follows:
The following automatic adjustment is performed within the model:
Parameter Fitting
The model includes the 4 fitable parameters F, vRV, vLV and k2. Please inspect the %SE standard error to get information about the reliability of the parameter estimates. The scale factor A (EF scale) and the exponent B (EF exp) of the extraction function can be entered as input parameters.
Reference
1. Lortie M, Beanlands RS, Yoshinaga K, Klein R, Dasilva JN, DeKemp RA: Quantification of myocardial blood flow with 82Rb dynamic PET imaging. Eur J Nucl Med Mol Imaging 2007, 34(11):1765-1774.