The Patlak plot has been developed for systems with irreversible trapping [17,18]. Most often it is applied for the analysis of FDG, which can be modeled as a 2-tissue compartment model with k4=0. The Patlak plot belongs to a group of graphical analysis techniques, whereby the measured TAC undergoes a transformation and is plotted against some sort of "normalized time".
The Patlak plot is given by the expression
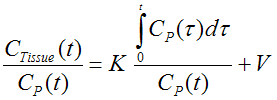
This means that the measured PET activity is divided by plasma activity, and plotted at a "normalized time" (integral of input curve from injection divided by instantaneous plasma activity). For systems with irreversible compartments this plot will result in a straight line after sufficient equilibration time. The slope and the intercept must be interpreted according to the underlying compartment model. For the FDG model mentioned, the slope equals K1k3/(k2+k3) and represents the influx, while the intercept V equals V0+vB with the distribution volume V0 of the reversible compartment C1 and the fractional blood volume vB .
Application of Patlak Plot as a Reference Method
When the plasma activity is not available, the Patlak plot can be employed as a reference method provided that there exists some tissue wherein tracer is not irreversibly trapped [42]. The procedure simply replaces Cplasma(t) in the above equation by the TAC of the reference tissue. Under several assumptions, including a common K1/k2, the slope of the linear regression represents the following relation
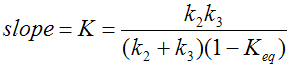
with the equilibrium constant Keq.
For instance, the Patlak plot has been applied in this way to calculate an index of the influx Ki of FDOPA using a cerebellum or occipital lobe TAC as the reference.
Implementation Notes
The Patlak Plot model calculates and displays the transformed measurements as described by the formula above. It allows fitting a regression line within a range defined by the parameters Start Lin. and End Lin. The results are the regression slope and the intercept. There is also an error criterion Max Err. to fit Start Lin. For instance, if Max Err. is set to 10% and the fit box of Start Lin. is checked, the model searches the earliest sample so that the deviation between the regression and all measurements is less than 10%. Samples earlier than the Start Lin. time are disregarded for regression and thus painted in gray.
For FDG data, the Lumped constant (LC) and the plasma glucose level (PG) of the patient should be entered. The metabolic rate of glucose MRGlu is then obtained from the regression slope by MRGlu = slope * PG / LC.
To use the Patlak Plot as a reference model in PKIN is very simple: a regional TAC can be copied to the plasma curve using the Region to input button in the Copy input curves tools, and then the Patlak Plot model selected.
Abstract [17]:
"A theoretical model of blood-brain exchange is developed and a procedure is derived that can be used for graphing multiple-time tissue uptake data and determining whether a unidirectional transfer process was dominant during part or all of the experimental period. If the graph indicates unidirectionality of uptake, then an influx constant (Ki) can be calculated. The model is general, assumes linear transfer kinetics, and consists of a blood- plasma compartment, a reversible tissue region with an arbitrary number of compartments, and one or more irreversible tissue regions. The solution of the equations for this model shows that a graph of the ratio of the total tissue solute concentration at the times of sampling to the plasma concentration at the respective times (Cp) versus the ratio of the arterial plasma concentration-time integral to Cp should be drawn. If the data are consistent with this model, then this graph will yield a curve that eventually becomes linear, with a slope of Ki and an ordinate intercept less than or equal to the vascular plus steady-state space of the reversible tissue region."