Monte Carlo Simulations

The purpose of performing Monte Carlo simulations in kinetic modeling is to get information about the standard error of the parameter values found in a fit. There are two different kinds of sources which contribute to the uncertainty of the parameters:

1. All the input data are measured and hence prone to measurement errors.
2. The model may contain more parameters than supported by the data, so that the effect of one parameter may be counter-balanced by another parameter.

The paradigm used for performing Monte Carlo simulations is described by Flannery et al. [11]. The basic idea is to simulate a series of measurements and statistically analyze the results when modeling these synthetic "measurements".

In PKIN Monte Carlo simulations can be performed for compartment models applied to a single tissue (Mt-Carlo) and models coupled across several tissues (Coupled Mt-Carlo) by selecting the respective panes.

Single Tissue

Three types of "noise" can be defined. For each "noise" the distribution type as well as the variance has to be configured. After selecting the distribution a dialog window appears for defining the variance as described in the Residual weighting for model fitting.

1. Blood noise to be added to the blood data for simulating noisy input curves. This option is only supported for blood models of type Lin. Interpolation.
2. Model noise to be added to the tissue model curve for simulating TAC noise. Note that here only the noise distribution needs to be selected. The noise variance is adopted from the Weigthing tab on the Tissue pane.
3. Parameter noise to be added to the starting parameters for disturbing the starting conditions from the ideal solution. For instance 20% noise can be added to the ideal parameter values.
   Three distributions are available for noise generation, Gaussian, Poisson and Uniform. They are applied for each individual measurement with the prescribed variance.

When the Start Monte Carlo button is selected the following processing starts:

1. An initial fit is performed. From then on it is assumed that the result parameters represent the "true" parameters, and the model curve represents the "true" measurement curve.
2. The number of Simulations times a noisy data set is prepared according to the definitions and then fitted. Noise is added to the "true" curve (and optionally the input curve). The "true" parameters, optionally disturbed by some noise, are used as starting values, and the fit to the noisy data performed. The resulting parameter values are recorded.
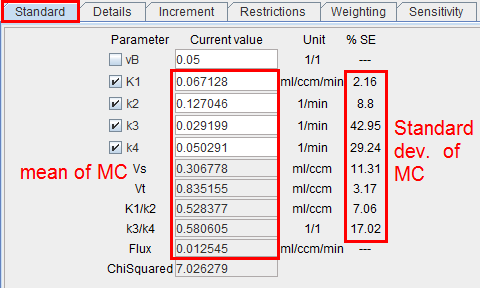
3. After all runs have completed, the distribution of the result parameters is analyzed resulting in a mean and a standard deviation value for each fitted parameter. These values are shown on the Standard tab of the Tissue page, and the model curve calculated with the mean parameters is shown. Often, it does not follow the measurement as well as with the fitted parameters. The Monte Carlo results should now be saved, because as soon as a parameter is changed or a new fit is initiated, the results get overwritten.
   

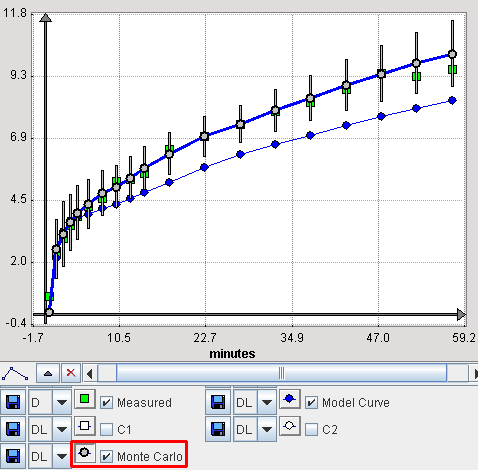
It is possible to visualize a summary of the fit results during the Monte Carlo runs by switching back from the Tissue to the Mt-Carlo pane. In the curve display, a new curve Monte Carlo appears with vertical bars. The end points of these bars mark the minimal and the maximal value that any of the resulting model curves reached at a particular time point.

Several Tissues Coupled

The same principle as for the single tissue Monte Carlo simulation applies to the Coupled Monte Carlo simulation (Coupled Mt- Carlo tab). In the upper section, the coupled parameters and the regions to couple are defined. In the lower section, blood and parameter noise can be specified. When starting, an initial coupled fit is performed to find the "true" parameters and the "true" model curves. Then, noisy curves are generated and coupled fits performed. At the end, the mean and standard errors are available as the regional parameters.