Water PET Model with Flow and Dispersion

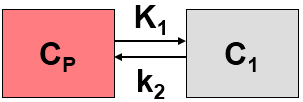
This model implements the 1-tissue compartment model for H₂¹⁵O water PET studies developed by E. Meyer [1].

Operational Model Curve

It is assumed that at by the arrival in tissue the true input curve C_p(t) has been dispersed. This dispersion is modeled by convolving C_p(t) with an exponential kernel

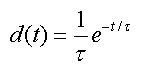
whereby the parameter t is called Dispersion. Incorporating the convolution into the 1-tissue compartment model and solving it using the Laplace transform yields the following analytic formula for the tissue concentration

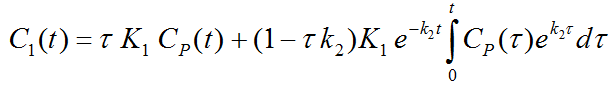
K₁ represents flow, and k₂ flow divided by the partition coefficient p.

The operational equation is given by

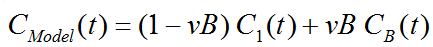
Note that in this particular case there is no difference between the plasma and blood concentrations C_p(t) and C_B(t) because water is a freely diffusible tracer.

Parameter Fitting

The tissue model includes four fitable parameters vB, K1 , k2, (Flow/Part.Coeff), t (Dispersion). Per default, however, v_B is fixed at vB=0 as in the original model. For water studies with the blood activity sampled in a peripheral artery, the resulting input curve is delayed respect to the arrival in tissue. In this case, the model should be fitted using the Fit region and blood delay button.

Implementation Note

Unlike the standard compartment models in PKIN the model curve of the operational equation is not calculated by integrating a set of differential equations, but rather using the analytical solution given above. The convolution integral is approximated by summing rectangles of 0.1sec in length, assuming that the acquisition time of dynamic water studies is short.

Reference

1. Meyer E: Simultaneous correction for tracer arrival delay and dispersion in CBF measurements by the H215O autoradiographic method and dynamic PET. J Nucl Med 1989, 30(6):1069-1078. PDF