Water PET Model with Flow and Dispersion

This model implements the 1-tissue compartment model for ¹H₂¹⁵O water PET studies.

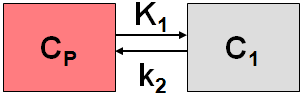
Additionally it is assumed that the true input curve has been convolved with a kernel

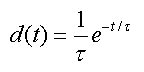
whereby the parameter t is called "Dispersion". This expression is incorporated into the 1-tissue compartment model and solved using the Laplace transform to yield the equation below, as described by E. Meyer [16].

The original operational equation

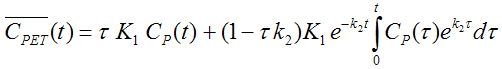
has been modified to

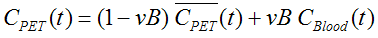
to allow for a spillover term. The interpretation for a freely diffusible model is: K₁ represents flow and k₂ is flow divided by the partition coefficient p.

Unlike the standard compartment models in PKIN the model curve of the operational equation is not calculated by integrating a set of differential equations, but rather using the analytical solution given above. This convolution integral is approximated by summing up rectangles of 0.1sec in length, assuming that the acquisition time of dynamic water studies is short.

Note: The delay parameter is not part of the TAC model, but as usual must be enabled for fitting in the input curve model.

Abstract [16]

"The difference in tracer arrival times between the radial artery and the brain following i.v. injection of 15O-labeled water plus the difference in dispersion of the tracer bolus between these two sites have to be accounted for in order to quantify cerebral blood flow by the autoradiographic approach and positron emission tomography (PET). We describe a method that simultaneously corrects for these two effects by means of a four-parameter fit to the dynamically acquired data. Unlike with other methods, where the two corrections are performed sequentially, no additional measurement of the dispersion time constant is required. We have validated and tested the method by means of simulations and application to data from six human studies. The mean dispersion time constant of 4.0 +/- 1.2 sec, estimated by the new method for the six studies, is in fair agreement with estimates of 3 to 5 sec derived from cardiac PET."

Compartment Models for Cardiac PET

Model Name	Description
Card. NH3 (Metabolite corr.)	As above, but the left ventricle input curve is linearly corrected for metabolites.
Card. NH3 (Geometrical corr.)	1-Tissue compartment model with two spillover terms. Has been developed for cardiac NH₃-PET studies with bolus administration.
Card. NH3 (2 Compartments)	2-Tissue compartment model with metabolic trapping. Has been developed for cardiac NH₃-PET studies with bolus administration.
Card. Rb-82 (1 Compartment)	1-compartment model for the quantification of myocardial perfusion with Rubidium-82 PET data.
Card. Rb-82 (2 Compartment)	Two-compartment model for the quantification of myocardial perfusion with Rubidium-82 PET data.
Card. H2O (Tissue fraction)	1-Tissue compartment model with two spillover terms. Has been developed for cardiac H₂¹⁵O- PET studies with bolus administration.
Card. H2O (Geometrical corr.)	As above, but with geometrical spillover correction.
Card. Acetate (1 Compartment)	1-compartment model for the quantification of myocardial perfusion with ¹¹C Acetate PET data.

Assumptions of the Cardiac Models

The cardiac models usually apply a geometrical spillover with two correction terms: correction for signal from the left and right ventricle.
For calculating the myocardial perfusion per g tissue using a density of 1.04 g/ml for myocardial tissue is applied.
Usually the PET signal from the left ventricle or the atrium is used as a measure of the tracer activity in blood. Depending on the tracer, corrections are applied to this blood curve for calculation the concentration of parent tracer with is required as the input curve of the models.

Exceptions to these rules are specified in the description of the individual models.